PID制御の基礎をPythonのライブラリの一種であるcontrolを使って勉強しましょう。
今回は、ミニ四駆などのおもちゃによく使われているDCモータの特性と回転制御をシミュレーションで確認します。
この記事を読めば、PID制御コントローラを用いたDCモータの制御モデル化とpythonを使った外乱応答のシミュレーションがわかります。
目次
PID制御ありの外乱を含んだDCモータモデル
前回の記事では、DCモータに環境変化による抵抗力などのトルク外乱が入った場合を考えてみました。
単純にDCモータの端子間に電圧を印加するだけの場合、外乱トルクが加わると回転数が落ち込んでしまい、所望の回転数を維持することができませんでした。
そこで今回はPID制御を使って外乱トルクが加わっても回転数を維持するようにしたいと思います。
ブロック線図は以下のようになります。
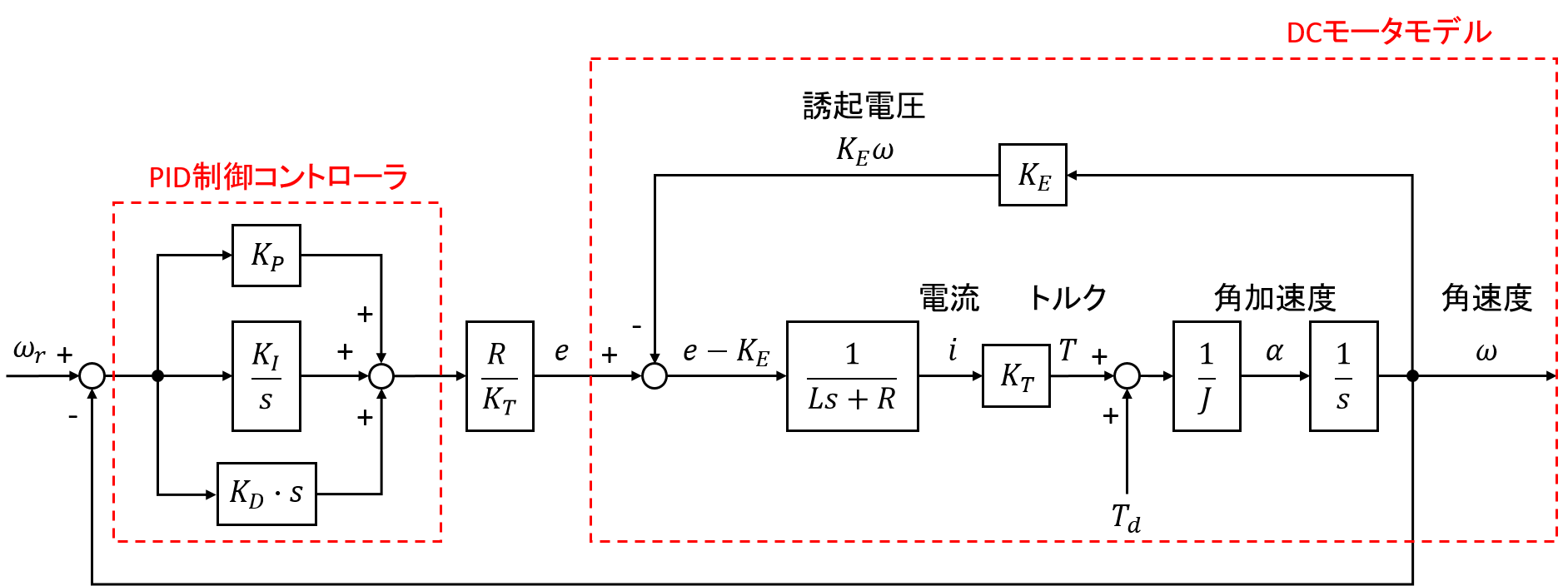
使用したpythonライブラリ
今回は以下のpythonライブラリを使用しました。
- control
- matplotlib
- numpy
- scipy
- pandas
python controlでシミュレーションするために伝達関数を等価変換する
.png)

2.png)
外乱トルクが入ったDCモータモデルのブロック線図を下図のように等価変換(簡単化)することができます。
PID制御ありのDCモータの回転制御シミュレーション
python controlを使ってPID制御ありのDCモータの外乱応答を確認する
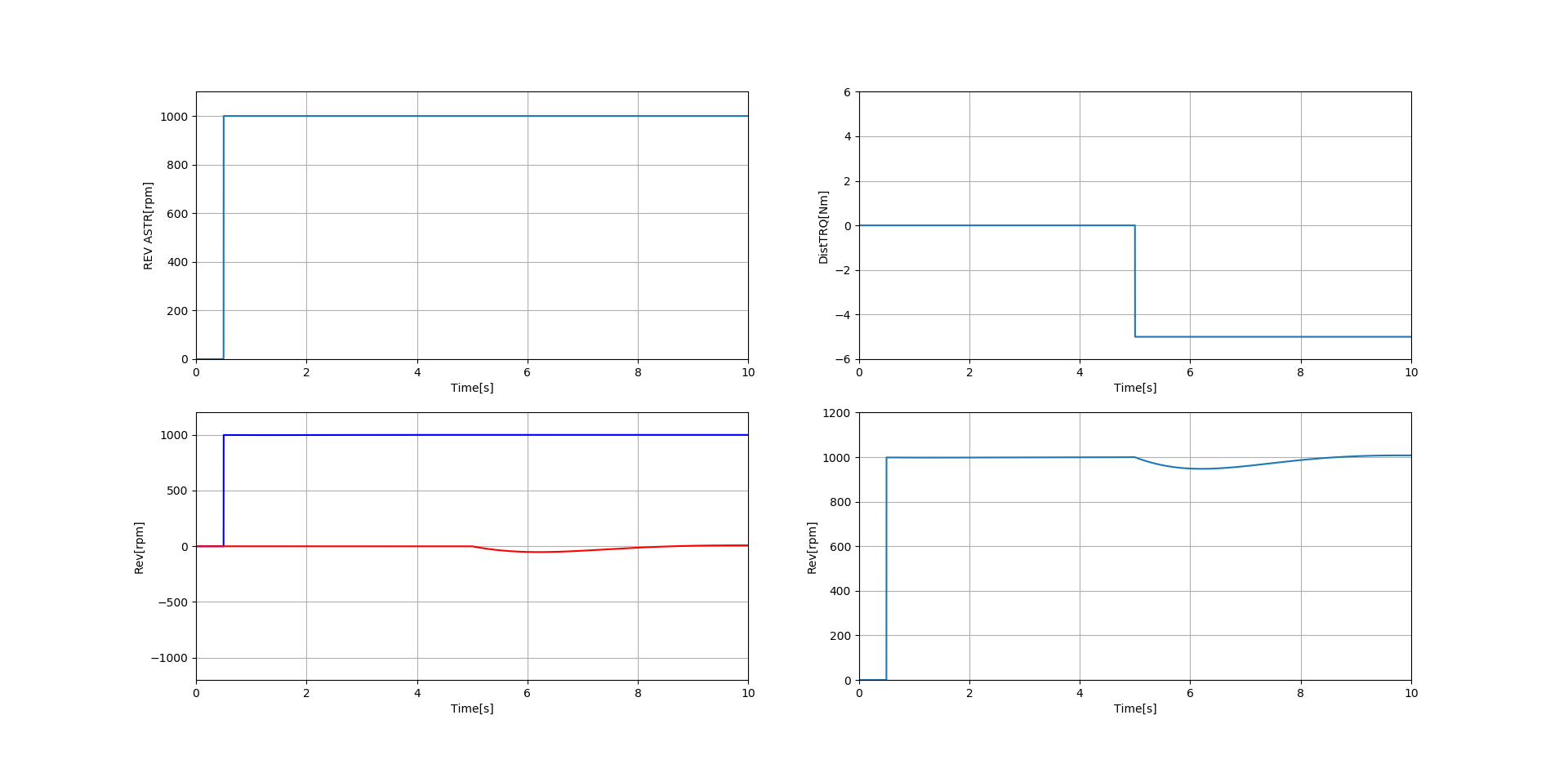
回転数指令値を0.5s時点で1000rpm入力し、外乱トルクを5s時点で-5Nm入力する場合をシミュレーションしてみます。
0.5s時点で左上の回転数指令値が0rpm → 1000rpmに変化しています。
左下の青線が目標値応答伝達関数の出力で、1000rpmに立ち上がっていることがわかります。
5s時点で右上の外乱トルクが-5Nm入力されています。
右下図が目標値応答と外乱応答を足し合わせた最終的な出力になります。
外乱トルクが入力された直後は回転数が落ち込んでいますが、すぐにPID制御が働き、回転数指令値の1000rpmを維持することができていることがわかります。
シミュレーションのpythonソースコード
今回入力データが『電圧目標値』と『外乱トルク』の2つを用意するため、csvファイルからデータを読み込んでいます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
"""DCモータの外乱応答(PID制御あり)""" from control.matlab import * import numpy as np from matplotlib import pyplot as plt from scipy import arange import pandas as pd """表示の設定""" mon_t_st = 0 mon_t_end = 10 """入力データの読み込み""" t = pd.read_csv('input_data_voltage.csv', usecols=[0]) print(t) u = pd.read_csv('input_data_voltage.csv', usecols=[1]) u = u*1000 # 1000rpmに調整 print(u) d = pd.read_csv('input_data_voltage.csv', usecols=[2]) d = d*(-5) # -5Nmに調整 print(d) plt.subplot(2,2,1) plt.plot(t,u) plt.grid(True) plt.xlabel('Time[s]') plt.ylabel('REV ASTR[rpm]') plt.xlim(mon_t_st,mon_t_end) plt.ylim(0,1100) plt.subplot(2,2,2) plt.plot(t,d) plt.grid(True) plt.xlabel('Time[s]') plt.ylabel('DistTRQ[Nm]') plt.xlim(mon_t_st,mon_t_end) plt.ylim(-6,6) """------------------------""" pi = np.pi # 円周率 """DCモータの特性パラメータ""" R = 0.65 # 回路の抵抗[Ω] L = 0.0021 # 回路のインダクタンス[H] J = 0.0005 # モータイナーシャ[kgm^2] Ke = 0.03 # 誘起電圧定数[V/(rad/s)] Kt = 0.03 # トルク定数[Nm/A] """------------------------""" """コントローラのパラメータ""" Kd = 0.5 Kp = 0.5 Ki = 0.5 """DCモータの伝達関数""" G1 = tf([Kd*R,Kp*R,Ki*R],[L*J,(R*J+Kd*R),(Kt*Ke+Kp*R),Ki*R]) G2 = tf([L,R,0],[L*J,(R*J+Kd*R),(Kt*Ke+Kp*R),Ki*R]) print(G1) print(G2) """------------------------""" #ステップ応答 (y1,t1,x1) = lsim(G1, u*2*3.14/60, t) (y2,t2,x2) = lsim(G2, d, t) yout = y1 + y2 y1 = y1*60/2/pi # [rad/s]→[rpm] y2 = y2*60/2/pi # [rad/s]→[rpm] y_rpm = yout*60/2/pi # [rad/s]→[rpm] plt.subplot(2,2,3) plt.plot(t1,y1,color='blue') plt.plot(t1,y2,color='red') plt.grid(True) plt.xlabel('Time[s]') plt.ylabel('Rev[rpm]') plt.xlim(mon_t_st,mon_t_end) plt.ylim(-1200,1200) plt.subplot(2,2,4) plt.plot(t2,y_rpm) plt.ylim(0,1200) plt.xlim(mon_t_st,mon_t_end) plt.grid(True) plt.xlabel('Time[s]') plt.ylabel('Rev[rpm]') plt.show() |
Python controlを使ったPID制御ありのDCモータの回転制御シミュレーション(外乱応答)まとめ
今回はDCモータに外乱トルクが加わった場合にPID制御を用いて回転数を維持できることをシミュレーションで確認しました。
最後まで読んでいただき、ありがとうございました。



コメント