PID制御の基礎をPythonのライブラリの一種であるcontrolを使って勉強しましょう。
今回は、主にノイズ除去などに用いられる低周波信号だけを通過させるフィルタであるローパスフィルタ(Low Pass Filter:LPF)について説明していきます。
【Python】PID制御をわかりやすく解説。Python controlを使って動きをグラフで説明します。【PID制御の基礎】
目次
ローパスフィルタ(LPF)とは?
ローパスフィルタ(Low Pass Filter)とは低周波信号(Low)だけを通過(Pass)させるフィルタ(Filter)のことです。
主に入力信号のノイズを除去する前処理として使われます。
センサなどから入力される信号には基本的にノイズが含まれています。
コントローラで制御する際にはノイズ成分を除去(前処理)して制御処理演算を実施することになります。
使用したpythonライブラリ
今回は以下のpythonライブラリを使用しました。
- control
- matplotlib
- numpy
- scipy
python controlを使ってローパスフィルタの動作を確認
python controlを使ってローパスフィルタのボード線図を描画
まずはローパスフィルタのボード線図(伝達特性)を描画してみましょう。
ローパスフィルタの伝達関数は以下です。
\[F(s) = \frac{1}{Ts+1}\]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
"""ローパスフィルタのボード線図を描画""" from control.matlab import * import numpy as np from matplotlib import pyplot as plt pi = np.pi # 円周率 T = 1/(2*pi*100) # フィルタ時定数 num = [1] # 分子の式 den = [T,1] # 分母の式 sys = tf(num, den) # 伝達関数 bode(sys) plt.show() # ボード線図を描画 |
上記pythonファイルを実行すると下図のボード線図が表示されます。
折点周波数は100Hz(フィルタ時定数Tで設定)にしています。
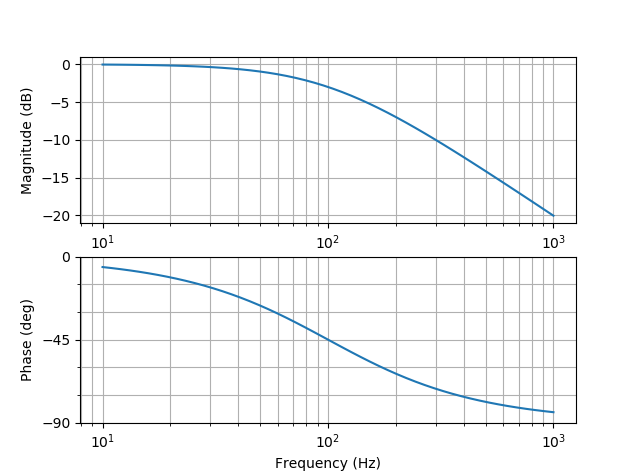
ゲインが20dB下がっている折点周波数から10倍以上の周波数でノイズ除去できます。
そのため、1kHz以上のノイズ成分を除去できるフィルタが設計できたことになります。
python controlを使ってローパスフィルタの時間軸応答を表示
先程設計したローパスフィルタの時間軸応答を確認してみましょう。
以下のソースコードでローパスフィルタのステップ応答を実行します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
"""ローパスフィルタのボード線図を描画""" from control.matlab import * import numpy as np from matplotlib import pyplot as plt from scipy import arange pi = np.pi # 円周率 T_LPF = 1/(2*pi*100) # フィルタ時定数 num = [1] # 分子の式 den = [T_LPF,1] # 分母の式 sys = tf(num, den) # 伝達関数 #ステップ応答 (y1,t1)=step(sys, T=arange(0, 0.01, 0.0001)) plt.plot(t1,y1) plt.show() |
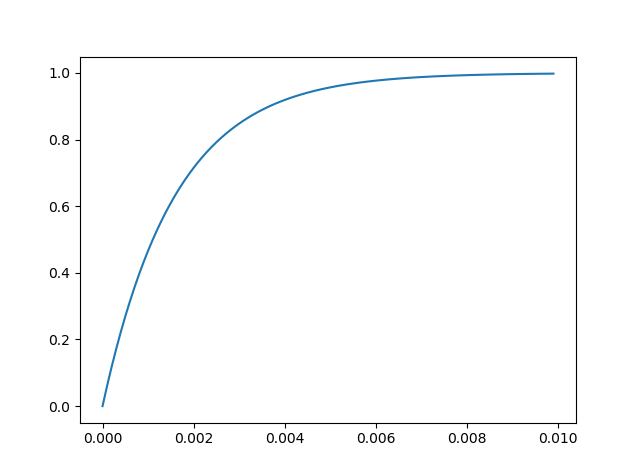
ローパスフィルタのステップ応答結果はこちらになります。
フィルタ時定数が1/(2*pi*100)[s]なので、約0.00159[s]で63.2%と設計値通りの応答となっています。
python controlを使ってローパスフィルタのノイズ除去性能を確認する
最後に、正弦波を入力してローパスフィルタのノイズ除去性能を確認しましょう。
10Hzと1kHzの合成正弦波をローパスフィルタに入力し、時間軸応答を確認します。
以下のソースコードでローパスフィルタの正弦波応答シミュレーションを実行します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
"""ローパスフィルタの時間軸応答を確認""" from control.matlab import * import numpy as np from matplotlib import pyplot as plt pi = np.pi # 円周率 T_LPF = 1/(2*pi*100) # フィルタ時定数 num = [1] # 分子の式 den = [T_LPF,1] # 分母の式 sys = tf(num, den) # 伝達関数 """入力信号:Sin波を生成""" omega1 = 2*pi*10 t = np.arange(0, 1, 0.0001) u1 = np.sin(omega1*t) # 10HzのSin波を生成 omega2 = 2*pi*1000 u2 = 0.2*np.sin(omega2*t) # 1kHzのSin波を生成 u = u1 + u2 # Sin波を合成 """シミュレーション実行""" [y1, t1, x1] = lsim(sys, U=u, T=t) """Figure表示""" plt.subplot(2,1,1) plt.plot(t,u) # 入力信号を表示 plt.grid(True) plt.xlim(0, 0.1) plt.ylim(-1.5, 1.5) plt.subplot(2,1,2) plt.plot(t1, y1) # 応答波形を表示 plt.grid(True) plt.xlim(0, 0.1) plt.ylim(-1.5, 1.5) plt.show() |
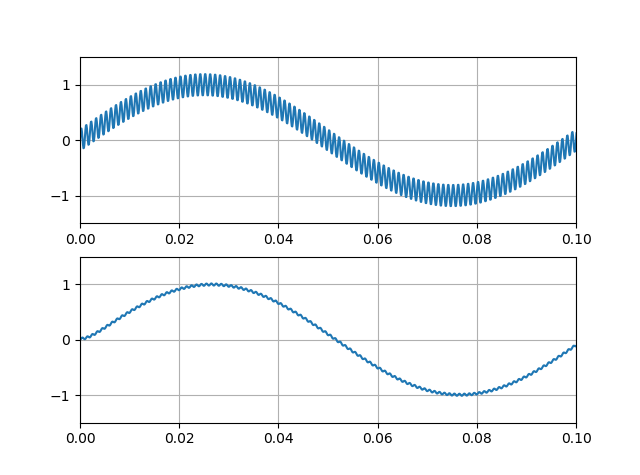
上図で細かくギザギザしているのが1kHzの信号成分です。
下図のローパスフィルタの応答波形では1kHzの信号成分が小さく(ノイズ除去)なっていることが確認できます。
Python controlを使ったローパスフィルタのまとめ
pythonのライブラリであるcontrolを使ってローパスフィルタの特性と応答シミュレーションができました。
実際にセンサなどで取得したデータはサンプリングされているため、ソフトウェアに実装する際には離散(デジタル)化する必要があります。
代表的な離散化手法であるTustin近似を用いた場合のローパスフィルタについては後日追記します。
最後まで読んでいただき、ありがとうございました。



コメント