PID制御の基礎をPythonのライブラリの一種であるcontrolを使って勉強しましょう。
今回は、ミニ四駆などのおもちゃによく使われているDCモータの特性と回転制御をシミュレーションで確認します。
この記事を読めば、DCモータのモデル化とpythonを使ったシミュレーションがわかります。
目次
DCCモータとは?
DCモータはDC(Direct Current)と付く通り、直流で駆動するモータです。
電気回路としてはRL回路と等価です。
機械としてはモータは回転運動を行います。
使用したpythonライブラリ
今回は以下のpythonライブラリを使用しました。
- control
- matplotlib
- numpy
- scipy
DCモータの基礎
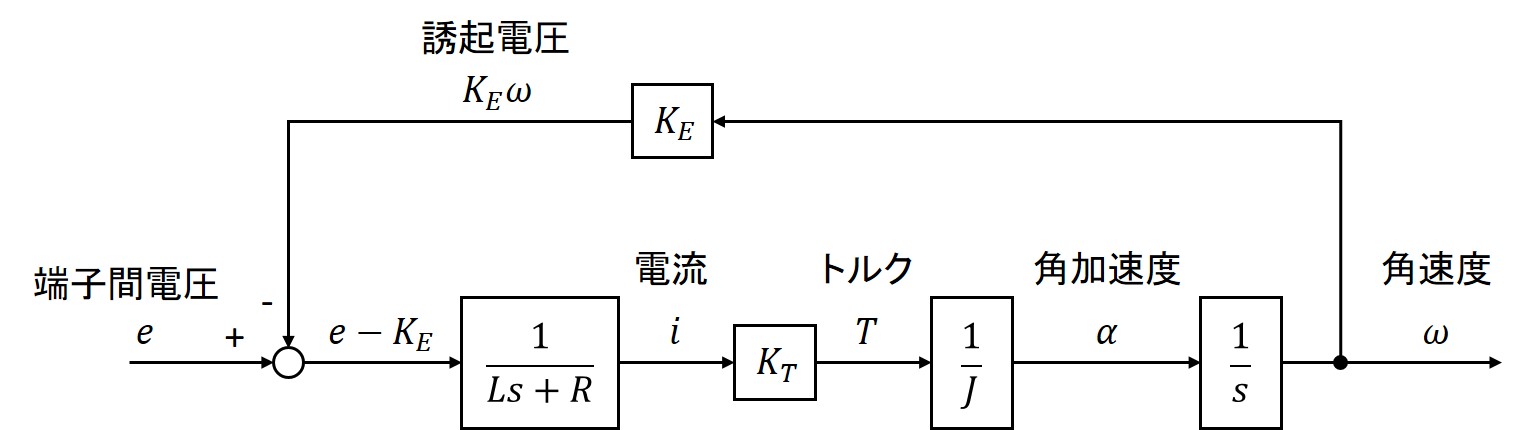
DCモータの特性をブロック線図で表現する
DCモータに生じる物理現象を数式で表します。
回路方程式:$$e + (-K_{E}\omega) + \left(-L\frac{di}{dt}\right) + (-Ri) = 0$$
トルクと電流の関係式:$$T = K_{T}i$$
運動方程式:$$T = J\alpha = J\frac{d\omega}{dt}$$
上の3式をブロック線図で表現すると以下のようになります。
python controlを使ってDCモータの時間軸応答を確認する
DCモータの端子間に電圧を1V印加したときのステップ応答を確認します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
"""DCモータの応答""" from control.matlab import * import numpy as np from matplotlib import pyplot as plt from scipy import arange pi = np.pi # 円周率 """DCモータの特性パラメータ""" R = 0.65 # 回路の抵抗[Ω] L = 0.0021 # 回路のインダクタンス[H] J = 0.0005 # モータイナーシャ[kgm^2] Ke = 0.03 # 誘起電圧定数[V/(rad/s)] Kt = 0.03 # トルク定数[Nm/A] """------------------------""" G1 = tf(1,[L,R])*Kt*tf(1,[J,0]) # (e-Ke)→ωの伝達特性 G2 = tf(Ke,1) # ω→Keωの伝達特性 Gp = feedback(G1, G2) # e→ωの伝達関数 print(Gp) #ステップ応答 (y1,t1)=step(Gp, T=np.arange(0, 3, 0.0001)) y_rpm = y1*60/2/pi # [rad/s]→[rpm] plt.plot(t1,y_rpm) plt.grid(True) plt.xlabel('Time[s]') plt.ylabel('Rev[rpm]') plt.xlim(0, 3) plt.ylim(0,350) plt.show() |
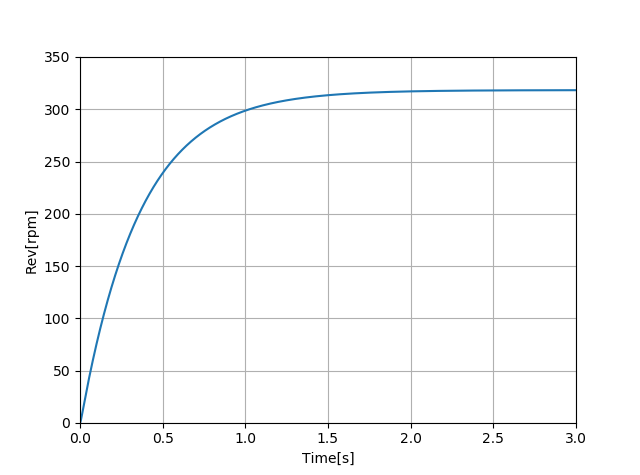
機械的時定数である約0.361[s]で応答していることがわかります。
機械的時定数とは電圧印加から回転数が応答するまでの時定数のことで下式で求まることができます。
$$t_{m} = \frac{RJ}{K_{T}K_{E}} = 0.361[s]$$
DCモータの端子間に電圧を印加することである一定の回転数に収束しています。
DCモータの端子間に印加する電圧を変えることでDCモータの回転数を変えることができそうですね。
ミニ四駆などのおもちゃが乾電池を繋げるだけで一定速度で走っているのを模擬したことになります。
Python controlを使ったDCモータの回転制御シミュレーションまとめ
今回はDCモータのモデル化と電圧を印加することにより回転数を制御できることを確認しました。
次回はPID制御コントローラを設計し回転数を制御したいと思います。
最後まで読んでいただき、ありがとうございました。



コメント